Question

Mark the statement either true (in all cases) or false (for at least one example). If false, construct a specific example to show that the statement is not always true. Such an example is called a counterexample to the statement. If the statement is true, give a justification. If v1,…,v4 are in R4 and {v1,v2,v3} is linearly dependent then {v1,v2,v3,v4} is also linearly dependent.

Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.

(A) True. Because v3 = 2v1 + v2, v4 must be the zero vector. Thus, the set of vectors is linearly dependent.
(B) True. The vector v3 is a linear combination of v1 and v2, so at least one of the vectors in the set is a linear combination of the others and set is linearly dependent.
(C) True. If c1 =2, c2 = 1, c3 = 1, and c4 = 0, then c1v1 + ........... + c4v4 =0. The set of vectors is linearly dependent.
(D) False. If v1 = __, v2 =___, v3 =___, and v4 = [1 2 1 2], then v3 = 2v1 + v2 and {v1, v2, v3, v4} is linearly independent.

Answer 1

Answer with Step-by-step explanation:

We are given that
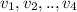`v_1,v_2,..,v_4` are in
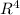`R^4` and
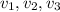`v_1,v_2,v_3` is linearly dependent then {v_1,v_2,v_3,v_4}[/tex] is also linearly dependent.

We have to find that given statement is true or false.

Dependent vectors:Dependent vectors are those vectors in which atleast one vector is a linear combination of other given vectors.

Or If we have vectors
`x_1,x_2,....x_n`

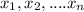
Then their linear combination

`a_1x_1+a_2x_2+.....+a_nx_n=0`

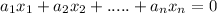
There exist at least one scalar which is not zero.

If
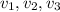`v_1,v_2,v_3` are dependent vectors then

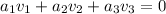`a_1v_1+a_2v_2+a_3v_3=0` for scalars
`a_1,a_2,a_3`

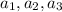
Then , by definition of dependent vectors

There exist a vector which is not equal to zero

If vector
`v_3` is a linear combination of
`v_1\;and \;v_2`, So at least one of vectors in the set is a linear combination of others and the set is linearly dependent.

Hence, by definition of dependent vectors

{
`v_1,v_2,v_3,v_4`} is linearly dependent.

Option B is true.