Question

What are the roots of the equation 2x^2+x=6​

Answer 1

(2x - 3)(x + 2)

Explanation:

Step 1 :

Equation at the end of step 1 :

(
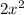`2x^(2)` + x) - 6

Step 2 :

Trying to factor by splitting the middle term

2.1 Factoring
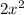`2x^(2)`+x-6

The first term is,
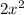`2x^(2)` its coefficient is 2 .

The middle term is, +x its coefficient is 1 .

The last term, "the constant", is -6

Step-1 : Multiply the coefficient of the first term by the constant 2 • -6 = -12

Step-2 : Find two factors of -12 whose sum equals the coefficient of the middle term, which is 1 .

-12 + 1 = -11

-6 + 2 = -4

-4 + 3 = -1

-3 + 4 = 1 That's it

Step-3 : Rewrite the polynomial splitting the middle term using the two factors found in step 2 above, -3 and 4

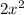`2x^(2)` - 3x + 4x - 6

Step-4 : Add up the first 2 terms, pulling out like factors :

x • (2x-3)

Add up the last 2 terms, pulling out common factors :

2 • (2x-3)

Step-5 : Add up the four terms of step 4 :

(x+2) • (2x-3)

Which is the desired factorization

(2x - 3)(x + 2)