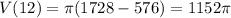Answer:
Suppose the bowl is situated such that the rim of the bowl touches the x axis, and the semicircular cross section of the bowl lies below the x-axis (in (iii) and (iv) quadrant ). Then the equation of the cross section of the bowl would be
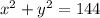 , where y≤ 0,
, where y≤ 0,
⇒
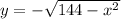
Here, h represents the depth of water,
Thus, by using shell method,
The volume of the disk would be,

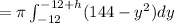
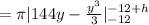
![=\pi [ (144(-12+h)-((-12+h)^3)/(3)-144(-12)+((-12)^3)/(3)}]](https://img.qammunity.org/2020/formulas/mathematics/college/q0ksm1pc1bnf867rq4mkpo7tm91f9w1qbw.png)
![=\pi [ -1728 + 144h - (1)/(3)(-1728+h^3+432h-36h^2)+1728-(1728)/(3)]](https://img.qammunity.org/2020/formulas/mathematics/college/lrxvq210e51of3ezfbfhcyhcm0zc3ula54.png)
![=\pi [ 144h - (1)/(3)(h^3+432h-36h^2}{3}]](https://img.qammunity.org/2020/formulas/mathematics/college/3yvgb93r2z8zpmxnxiw77jpoyzwx3s5sk0.png)
![=\pi [ 144h - (h^3)/(3) - 144h + 12h^2]](https://img.qammunity.org/2020/formulas/mathematics/college/n2i34lt0ub6rzdmi134s7hdhaquxox7tc2.png)

Special cases :
If h = 0,

If h = 12,