Question

A 12.0-cm long cylindrical rod has a uniform cross-sectional area A = 5.00 cm2. However, its density increases linearly from 2.60 g/cm3 at one end to 18.5 g/cm3 at the other end. This linearly increasing density can be described using the equation ???? = B + Cx. (a) Find the constants B and C required for this rod, assuming the low-density end is placed at x = 0 cm and the high-density end is at x = 12 cm. (b) The mass of the rod can be found using:m=dV=Adx=(B+Cx)Adx

Answer 1

(a) The constants required describing the rod's density are B=2.6 and C=1.325.

(b) The mass of the road can be found using
`A\int_0^(12)\left(B+Cx)dx`

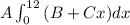
Step-by-step explanation:

(a) Since the density variation is linear and the coordinate x begins at the low-density end of the rod, we have a density given by

`2.6(g)/(cm^3)+(18.5(g)/(cm^3)-2.6(g)/(cm^3))/(12 cm)x = 2.6(g)/(cm^3)+1.325x(g)/(cm^2)`

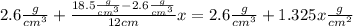
recalling that the coordinate x is measured in centimeters.

(b) The mass of the rod can be found by having into account the density, which is x-dependent, and the volume differential for the rod:

`m=\int\rho dv=\int\left(B+Cx\right)Adx=5\int_0^(12)\left(2.6+1.325x\right)dx=126.6`,

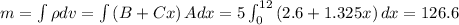hence, the mass of the rod is 126.6 g.