Question

Assume that the readings on scietific thermometers are normally distributed with a mean of 0 0C and a standard deviation of 1 0C . A thermometer is randomly selected and tested. Find the probability of the reading greater than -1.05 in degrees Celsius. (up to four decimal place, please)

Answer 1

Answer: 0.8531

Explanation:

Let x be the random variable that represents the readings on scientific thermometers .

Given : The readings on scientific thermometers are normally distributed,

Population mean :
`\mu=0^(\circ)\ C`

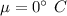
Standard deviation :
`\sigma=1^(\circ)\ C`

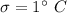
Z-score :
`z=(x-\mu)/(\sigma)`

Now, the z-value corresponding to -1.05 :
`z=(-1.05.-0)/(1)=-1.05`

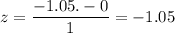
P-value =
`P(x>-1.05)=P(z>-1.05)=1-P(z\leq-1.05)`

`=1-0.1468591=0.8531409\approx0.8531\text{ (Rounded to four decimal places)}`

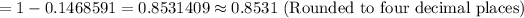
Hence, the probability of the reading greater than -1.05 in degrees Celsius.= 0.8531