Question

A hospital claims that the proportion, p, of full-term babies born in their hospital that weigh more than 7 pounds is 36%. In a random sample of 170 babies born in this hospital, 56 weighed over 7 pounds. Is there enough evidence to reject the hospital's claim at the level of significance?

Answer 1

Claim :The proportion, p, of full-term babies born in their hospital that weigh more than 7 pounds is 36%.

n = 170

x = 56

We will use one sample proportion test

`\widehat{p}=(x)/(n)`

`\widehat{p}=(56)/(170)`

`\widehat{p}=0.3294`

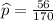
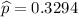
The proportion, p, of full-term babies born in their hospital that weigh more than 7 pounds is 36%.

`H_0:p \\eq 0.36 \\H_a:p= 0.36`

Formula of test statistic =
`\frac{\widehat{p}-p}{\sqrt{(p(1-p))/(n)}}`

`=\frac{0.3294-0.36}{\sqrt{(0.36(1-0.36))/(170)}}`

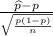
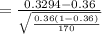
=−0.8311

Now refer the p value from the z table

P-Value is .202987 (Calculated by online calculator)

Level of significance α = 0.05

Since p value < α

So we reject the null hypothesis .

Hence the claim is true