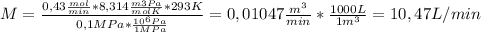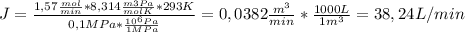Question

A permeation membrane separates an inlet air stream, F, (79 mol% N2, 21 mol% O2), into a permeate stream, M, and a reject stream, J. The inlet stream conditions are 293 K, 0.5 MPa, and 2 mol/min; the conditions for both outlet streams are 293 K and 0.1 MPa. If the permeate stream is 50 mol% O2, and the reject stream is 13 mol% O2, what are the volu- metric flowrates (L/min) of the two outlet streams?

Answer 1

• Permeate stream: M=10,47 L/min
• Reject stream: J=38,24 L/min

Step-by-step explanation:

Using the law of mass conservation, we have that the moles of any component in the inlet air stream equals the moles of this compenent in the two outlets stream. Being A the mole flowrate for the permeate stream and B the mole flowrate for the reject stream (both in mol/min), we have equation (1) and (2):

• Oxygen:

2 mol/min * 0,21 = A mol/min * 0,50 + B mol/min * 0,13 ......................(1)

0,42 = 0,5A + 0,13B...........................(1)

• Nitrogen:

2 mol/min * 0,79 = A mol/min * 0,50 + B mol/min * 0,87 ......................(2)

1,58 = 0,5A + 0,87B...........................(2)

Solving this system:

1,58 = 0,5A + 0,87B...........................(2)

0,42 = 0,5A + 0,13B...........................(1)

1,16 = 0A + 0,74B...............................(2) - (1)

1.16=0,74B

1,16/0,74=B

B=1,57 mol/min

And now replacing B in equation (1):

1,58 = 0,5A + 0,87*1,57

1,58-1,37=0,5A

0,21/0,5=A

A=0,43 mol/min

To calculate the volumetric flowrate of the permeate stream (M) and the reject stream (J), we just replace the given and calculate data into the ideal gas equation:

PV=nRT,.................... V = nRT/P

• Permeate stream:

`M= (0,43 (mol)/(min)*8,314(m3Pa)/(molK)*293K  )/(0,1 MPa*(10^(6)Pa )/(1 MPa) )=0,01047(m^(3) )/(min) * (1000 L)/(1 m^(3) )=10,47 L/min`

• Rejct stream:

`J= (1,57 (mol)/(min)*8,314(m3Pa)/(molK)*293K  )/(0,1 MPa*(10^(6)Pa )/(1 MPa) )=0,0382(m^(3) )/(min) * (1000 L)/(1 m^(3) )=38,24 L/min`