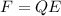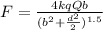Question

Four charges of magnitude +q are placed at the corners of a square whose sides have a length d. What is the magnitude of the total force exerted by the four charges on a charge Q located a distance b along a line perpendicular to the plane of the square and equidistant from the four charges?

Answer 1

The magnitude of the force exerted by object W on object Z is F.

Step-by-step explanation:

The magnitude of the force exerted by object W on object Z can be determined by analyzing the geometry and the charges involved. Since objects X and Z are at the midpoints of the sides of the square, they are equidistant from all four charges. As a result, the magnitude of the force exerted by each charge on object Z will be the same as the magnitude of the force exerted by each charge on object X. Therefore, the magnitude of the force exerted by object W on object Z is also F.

Answer 2

`F = (4kqQb)/((b^2 + (d^2)/(2))^(1.5))`

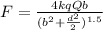
Step-by-step explanation:

Since all the four charges are equidistant from the position of Q

so here we can assume this charge distribution to be uniform same as that of a ring

so here electric field due to ring on its axis is given as

`E = (k(4q)x)/((x^2 + R^2)^(1.5))`

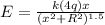
here we have

x = b

and the radius of equivalent ring is given as the distance of each corner to the center of square

`R = (d)/(\sqrt2)`

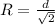
now we have

`E = (4kq b)/((b^2 + (d^2)/(2))^(1.5))`

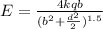
so the force on the charge is given as

`F = QE`

`F = (4kqQb)/((b^2 + (d^2)/(2))^(1.5))`