1) 9.18 s
In the first part of the motion, the rocket accelerates at a rate of
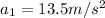
For a time period of
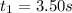
So we can calculate the velocity of the rocket after this time period by using the SUVAT equation:
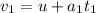
where u = 0 is the initial velocity of the rocket. Substituting a1 and t1,
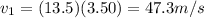
In the second part of the motion, the rocket decelerates with a constant acceleration of
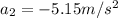
Until it comes to a stop, to reach a final velocity of
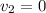
So we can use again the same equation
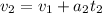
where
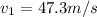 . Solving for t2, we find after how much time the rocket comes to a stop:
. Solving for t2, we find after how much time the rocket comes to a stop:

2) 299.9 m
We have to calculate the distance travelled by the rocket in each part of the motion.
The distance travelled in the first part is given by:
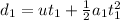
Using the numbers found in part a),
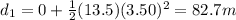
The distance travelled in the second part of the motion is
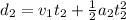
Using the numbers found in part a),
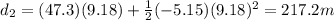
So, the total distance travelled by the rocket is
d = 82.7 m + 217.2 m = 299.9 m