Question

Water leaks out of a 3,200-gallon storage tank (initially full) at the rate V '(t) = 80 -t, where t is measured in hours and V in gallons. a. How much water leaked out between 10 and 20 hours? b. How long will it take the tank to drain completely?

Answer 1

water leak is 650 gallons

time required to full drain is 80 hrs

Step-by-step explanation:

given data

volume V = 3200 gallon

rate = V(t) = 80 - t

to find out

how much water leak between 10 and 20 hour and drain complete

solution

we know here rate is 80 - t

so here rate will be

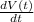`(dV(t))/(dt)` = 80 - t

and for time 10 and 20 hour

take integrate between 10 and 20

so water leak =
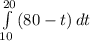`\int\limits^ {20}_ {10} {(80-t)} \, dt` .....................1

water leak = ( 80t -
`(t^(2) )/(2) )^(20)_(10)`

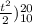
water leak = 650

so water leak is 650 gallons

and

we know here for full tank drain condition

water leak full = 80 t -
`(t^(2) )/(2)`

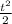
3200 = 80 t -
`(t^(2) )/(2)`

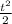
6400 = t² - 160 t

t = 80

so time required to full drain is 80 hrs