Question

A small metal sphere of mass 3.1 g and charge 2.6 μC is fired with an initial speed of 5.6 m/s directly toward the center of a second metal sphere carrying charge 3.4 μC. This second sphere is held fixed. If the spheres are initially a large distance apart, how close do they get to each other? Treat the spheres as point charges.

Answer 1

d = 1.636 m

Step-by-step explanation:

Initially charged sphere are far apart so their potential energy is zero . Kinetic energy will be of small sphere

K E of small sphere

= 1/2 m v²

= .5 x 3.1 x 10⁻³ x ( 5.6)²

=48.608 x 10⁻³ J

If d be the distance of closest approach between them , potential energy of

Charges

= k q₁ x q₂ / d²

`(9*10^9*2.6*10^(-6)*3.4*10^(-6))/(d^2)`

=
`(79.56*10^(-3))/(d^2)`

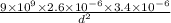
Total kinetic energy at this point will be zero.

Applying the theory of conservation of mechanical energy

Potential energy at distance d = Kinetic energy at infinity

48.608 x 10⁻³ =
`(79.56*10^(-3))/(d^2)`

d = 1.636 m