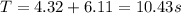Question

A car starts from rest and accelerates at a constant rate until it reaches 70 mi/hr in a distance of 220 ft, at which time the clutch is disengaged. The car then slows down to a velocity of 40 mi/hr in an additional distance of 480 ft with a deceleration which is proportional to its velocity. Find the time t for the car to travel the 700 ft.

Answer 1

`T = 10.43 s`

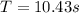
Step-by-step explanation:

During deceleration we know that the deceleration is proportional to the velocity

so we have

`a = - kv`

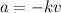
here we know that

`(dv)/(dt) = - kv`

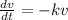
so we have

`(dv)/(v) = -k dt`

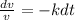
now integrate both sides

`\int (dv)/(v) = -\int kdt`

`ln((v)/(v_o)) = - kt`

`ln((40)/(70)) = - k(t)`

`kt = 0.56`

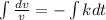
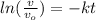
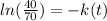
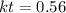
Also we know that

`a = (vdv)/(ds)`

`-kv = (vdv)/(ds)`

`\int dv = -\int kds`

`(v - v_o) = -ks`

`(40 - 70)mph = - k (480 ft)`

`-30 mph = -k(0.091 miles)`

`k = 329.67`

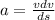
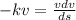
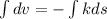
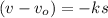
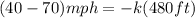
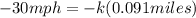
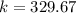
so from above equation

`t = (0.56)/(329.67) = 1.7 * 10^(-3) h`

`t = 6.11 s`

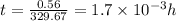
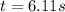
initially it starts from rest and uniformly accelerate to maximum speed of 70 mph and covers a distance of 220 ft

so we have

d = 220 ft = 67 m = 0.042 miles[/tex]

now we know that

`d = (v_f + v_i)/(2) t`

`0.042 = (70 + 0)/(2) t`

`t = 4.32 s`

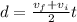
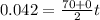
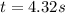
so total time of motion is given as

`T = 4.32 + 6.11 = 10.43 s`