Question

A piecewise function is shown below

g(x) = { -3x^2 -2x+8 for -4 ≦ x < 1

-2x+7p for 1 ≦ x ≦ 5


(a) for what value of p will the function be continuous
(b) Because one piece stops and the next piece starts at the point identified in part a, the pieces can be set equal to each other to find p. Fine p. Show your work. If you did everything on a calculator, explain the steps you took and include screenshots of each step.

Answer 1

p = 5/7

Explanation:

The given function is:

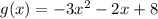`g(x) = -3x^(2) - 2x + 8` for -4 ≦ x < 1

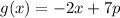`g(x) = -2x + 7p` for 1 ≦ x ≦ 5

Part a)

A continuous function has no breaks, jumps or holes in it. So, in order for g(x) to be continuous, the point where g(x) stops during the first interval -4 ≦ x < 1 must be equal to the point where g(x) starts in the second interval 1 ≦ x ≦ 5

The point where, g(x) stops during the first interval is at x = 1, which will be:

`-3(1)^(2)-2(1)+8=3`

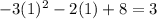
The point where g(x) starts during the second interval is:

`-2(1)+7(p) = 7p - 2`

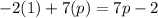
For the function to be continuous, these two points must be equal. Setting them equal, we get:

3 = 7p - 2

3 + 2 = 7p

p =
`(5)/(7)`

Thus the value of p for which g(x) will be continuous is
`(5)/(7)`.

Part b)

We have to find p by setting the two pieces equal to each other. So, we get the equation as:

`-3x^(2)-2x+8=-2x+7p\\\\ -3x^(2)+8=7p`

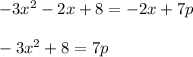
Substituting the point identified in part (a) i.e. x=1, we get:

`-3(1)^(2)+8=7p\\\\ 5=7p\\\\ p=(5)/(7)`

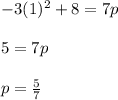
This value agrees with the answer found in previous part.