Question

A sample of lake water was analyzed to determine the amount of metals found in the lake. The standard deviation of the sampling method was found to be ±6.0%±6.0% . The standard deviation of the analytical method used to determine the amount of metals in the sample was determined to be ±2.4%±2.4% . What is the overall standard deviation?

Answer 1

The overall standard deviation, s = 6.46 %

Given:

Sampling variance,
`s_(b) = \pm 6.0% = 0.06`

Analytical variance,
`s_(a) = \pm 2.4% = 0.024`

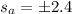
Solution:

Variance additive is given by:

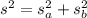`s^(2) = s_(a)^(2) + s_(b)^(2)` (1)

where

s = overall variance

Also, we know that:

Standard Deviation,
`\sigma = √(variance)`

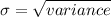
Therefore the standard deviation of the sampling, analytical and overall sampling is given by taking the square root of eqn (1) on both the sides:

`s = \sqrt{s_(a)^(2) + s_(b)^(2)}`

`s = \sqrt{0.024^(2) + 0.06^(2)} = 0.0646`

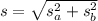
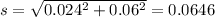
s = 6.46 %