Answer:
Step 3.
Explanation:
The given expression is
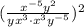
Step 1: Using distributive property of exponent we get
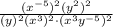
![[\because (ab)^x=a^xb^x]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/qxmpiro6f4mxcacibpm50yzx15afsx94ew.png)
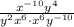
Ste 2: Using product property of exponent, we get

![[\because a^ma^n=a^(m+n)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/nq3mx7h59riuovldnajkcjliesnhhlzghy.png)
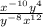
Step 3: Using quotient property of exponent, we get
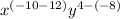
![[\because (a^m)/(a^n)=a^(m-n)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/3xqhwqy0w6z2mf6nqknwcxqwlgj93vihb0.png)

Therefore, the first incorrect step is 3.