Question

A large asteroid of mass 98700 kg is at rest far away from any planets or stars. A much smaller asteroid, of mass 780 kg, is in a circular orbit about the first at a distance of 201 meters as a result of their mutual gravitational attraction. What is the speed of the second asteroid?

Answer 1

1.81 x 10^-4 m/s

Step-by-step explanation:

M = 98700 kg

m = 780 kg

d = 201 m

Let the speed of second asteroid is v.

The gravitational force between the two asteroids is balanced by the centripetal force on the second asteroid.

`(GMm)/(d^(2))=(mv^2)/(d)`

`v=\sqrt{(GM)/(d)}`

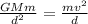
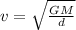
Where, G be the universal gravitational constant.

G = 6.67 x 10^-11 Nm^2/kg^2

`v=\sqrt{(6.67 * 10^(-11)* 98700)/(201)}`

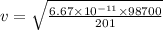
v = 1.81 x 10^-4 m/s