Question

Mallie

Date
8. Travel Times Journal found that the average per person cost of a
ound that the average per person cost of a 10-day trip along the Pacific
Coast, per person, is $1,015. This includes transportation, food, lodging, and entertainment.
a. If the data is normally distributed with standard deviation $198, find
ard deviation $198, find the percent of
Vacationers who spent less than $1.200 per day. Round to the nearest hundredth of a
percent.

Answer 1

82.38%

Explanation:

Average cost = u = $ 1,015

Standard Deviation =
`\sigma` = $ 198

Its given that data is normally distributed. We have to find what percentage of vacationers spend less than $ 1200.

Since the data is normally distributed, we can use the concept of z score to answer this question.

We have to find:

Probability ( Spending < 1200)

In symbolic form, this can be represented as:

P(X < 1200)

The formula for the z score is:

`z=(x-u)/(\sigma)`

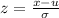
Using the values in this formula, we get:

`z=(1200-1015)/(198)=0.93`

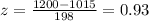
Thus,

P(X < 1200) is equivalent to P(z < 0.93)

From the z table we can find the probability of z scores being less than 0.93 to be 0.8238

Thus,

P(z < 0.93) = 0.8238

Since,

P(X < 1200) = P(z < 0.93), we can conclude:

The percent of Vacationers who spent less than $1,200 is 0.8238 or 82.38%