Answer:
time required after impact for a puck is 2.18 seconds
Step-by-step explanation:
given data
mass = 30 g = 0.03 kg
diameter = 100 mm = 0.1 m
thick = 0.1 mm = 1 ×
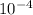 m
m
dynamic viscosity = 1.75 ×
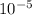 Ns/m²
Ns/m²
air temperature = 15°C
to find out
time required after impact for a puck to lose 10%
solution
we know velocity varies here 0 to v
we consider here initial velocity = v
so final velocity = 0.9v
so change in velocity is du = v
and clearance dy = h
and shear stress acting on surface is here express as
= µ
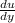
so
= µ
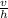 ............1
............1
put here value
= 1.75×
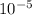 ×
×

= 0.175 v
and
area between air and puck is given by
Area =

area =
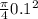
area = 7.85 ×
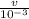 m²
m²
so
force on puck is express as
Force = × area
force = 0.175 v × 7.85 ×

force = 1.374 ×
 v
v
and now apply newton second law
force = mass × acceleration
- force =
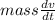
- 1.374 ×
 v =
v =
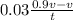
t =

time = 2.18
so time required after impact for a puck is 2.18 seconds