Question

In certain ranges of a piano keyboard, more than one string is tuned to the same note to provide extra loudness. For example, the note at 110 Hz has two strings at this frequency. If one string slips from its normal tension of 602 N to 564.00 N, what beat frequency is heard when the hammer strikes the two strings simultaneously? beats/s

Answer 1

Step-by-step explanation:

Given that,

Frequency in the string, f = 110 Hz

Tension, T = 602 N

Tension, T' = 564 N

We know that frequency in a string is given by :

`f=(1)/(2L)\sqrt{(T)/(m/L)}`, T is the tension in the string

i.e.

`f\propto√(T)`

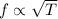
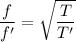`(f)/(f')=\sqrt{(T)/(T')}`, f' is the another frequency

`{f'}=f* \sqrt{(T')/(T)}`

`{f'}=110* \sqrt{(564)/(602)}`

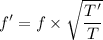
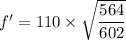
f' =106.47 Hz

We need to find the beat frequency when the hammer strikes the two strings simultaneously. The difference in frequency is called its beat frequency as :

`f_b=|f-f'|`

`f_b=|110-106.47|`

`f_b=3.53\ beats/s`

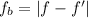
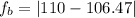
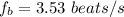
So, the beat frequency when the hammer strikes the two strings simultaneously is 3.53 beats per second.