Question

A charge of +3.00 μC is located at the origin, and a second charge of -2.00 μC is located on the x-y plane at the point (50.0 cm, 60.0 cm). 1) Determine the x-component of the electric force exerted by the -2.00 μC charge on the +3.00 μC charge. (Express your answer to three significant figures.)

Answer 1

0.0567 N

Step-by-step explanation:

q1 = 3 micro coulomb

q2 = - 2 micro coulomb

OB = 50 cm

AB = 60 cm

By using Pythagoras theorem in triangle OAB

`OA^(2)=OB^(2)+AB^(2)`

`OA^(2)=50^(2)+60^(2)=6100`

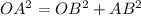
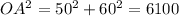
OA = 78.1 cm

By using the Coulomb's law, the force on 3 micro coulomb due to -2 micro coulomb is

`F=\frac {Kq_(1)q_(2)}{OA^(2)}= \frac{9 * 10^(9)}* 3* 10^(-6) * 2 * 10^(-6){0.781^(2)}`

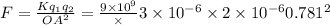
F = 0.0885 N

The horizontal component of force is

= F CosФ =
`F* (OB)/(OA)`

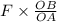
= 0.0885 x 50 / 78.1 = 0.0567 N