Question

Which of the following properties can be used to show that the expression 4^5/3 is equivalent to ^3√4^5

Answer 1

`\sqrt[3]{4^5}=(4^5)^{(1)/(3)}=4^{(5)/(3)}`

Option 1 and Option 3 is correct

Explanation:

Given:
`4^{(5)/(3)}=\sqrt[3]{4^5}`

This is exponent to radical change property.

The fraction exponent write as radical.

`a^{(m)/(n)}=\sqrt[n]{a^m}`

• Option 1: Radical to exponent

`\sqrt[3]{4^5}=(4^5)^{(1)/(3)}=4^{(5)/(3)}`

True

• Option 2: Addition of exponent if base is same.

`4^{(8)/(3)}\cdot 4^{(7)/(3)}=4^{{(8)/(3)+(7)/(3)}=4^5`

False

• Option 3: Multiply exponent to exponent, True
• Option 4: Division property of exponent, False

Answer 2

Answer: First option.

Explanation:

For this exercise it is importnatn to to remember the properties that are shown below:

1)
`a^(1)/(n)=\sqrt[n]{a}`

2)
`(a^m)^n=a^((mn))`

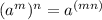
Therefore, given the following expression provided in the exercise:

`\sqrt[3]{4^5}`

You can apply the properties mentioned before, in order to find an equivalent expression.

Therefore, you get:

`\sqrt[3]{4^5}=(4^5)^{(1)/(3)}=4^{(5*1)/(3)}=4^{(5)/(3)}`

Then the answer is the first option.