Question

A 10000 kg rocket blasts off vertically from the launch pad with a constant upward of 2.25 m/s2 and feels no appreciable air resistance. When it has reached a height of 525 m, its engine suddenly fails so that only gravity acts on it after that. What is the maximum height that the rocket reaches?

Answer 1

The maximum height that the rocket reaches is 645.5 m.

Step-by-step explanation:

Given that,

Mass = 10000 kg

Acceleration = 2.25 m/s²

Distance = 525 m

We need to calculate the velocity

Using equation of motion

`v^2=u^2+2as`

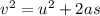
Put the value in the equation

`v^2=0+2\time2.25*525`

`v=√(2*2.25*525)`

`v=48.60\ m/s`

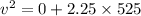
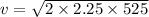
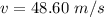
We need to calculate the maximum height with initial velocity

Using equation of motion

`v^2=u^2-2gh`

`h=(v^2-u^2)/(-2g)`

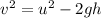
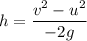
Put the value in the equation

`h=(0-(48.60)^2)/(-2*9.8)`

`h=120.50\ m`

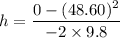
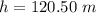
The total height reached by the rocket is

`h'=s+h`

`h'=525+120.50`

`h'=645.5\ m`

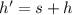
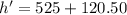
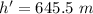
Hence, The maximum height that the rocket reaches is 645.5 m.