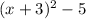Question

Which is equivalent to the expression? x2 + 6x + 4 A) (x + 3)2 + 5 B) (x + 3)2 − 5 C) (x − 3)2 + 5 D) (x − 3)2 − 5

Answer 1

Explanation:

(x + 3)² − 5 because :

(x + 3)² − 5 = x² +6x+9 -5 =x²+6x+4

Answer 2

B)
`(x + 3)^2 - 5`

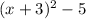
Explanation:

the equation is:
`x^2 + 6x + 4`

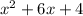
we have an equation of the form

`ax^2+bx+c`

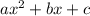
where

`a=1,b=6,c=4`

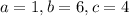
and we must complete the square to obtain a perfect square binomial,

we must add and substract the following:

`((b)/(2a) )^2`

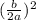
which is:

`((6)/(2*1) )^2=3^2`

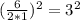
and then the equation becomes:

`x^2 + 6x + 4+3^2-3^2`

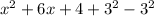
where the terms
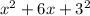`x^2+6x+3^2` are the components of the perfect square binomial:
`(x+3)^2`

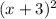
and thus, the equation now is:

`(x+3)^2+4-3^2\\=(x-3)^2+4-9\\=(x+3)^2-5`

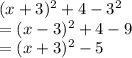
the answer is: B)
`(x + 3)^2 - 5`