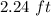Answer: Paul used the square tile with the greatest side length. Its side length (to the nearest hundredth) was
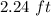
Explanation:
The side lenght "s" of a square can be calculated with this formula:
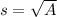
Where "A" is the area.
We know that Thomas used 25 square tiles to cover a patio with an area of 75 square feet, then, the area of each 1 tile was:

Its side lenght, rounded to the nearest hundreth,was:
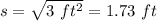
Paul used 20 square tiles to cover a patio with an area of 100 square feet, then, the area of each 1 tile was:
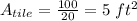
Its side lenght, rounded to the nearest hundreth,was:
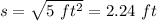
Sarah used 30 square tiles to cover a patio with an area of 120 square feet, then, the area of each 1 tile was:
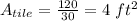
Its side lenght, rounded to the nearest hundreth,was:

Therefore, Paul used the square tile with the greatest side length. Its side length (to the nearest hundredth) was