Question

The output of an ac generator connected to an RLC series combination has a frequency of 12 kHz and an amplitude of 28 V. If R = 4.0 Ohms, L = 30 μH, and C = 800 nF, find a. The impedance b. The amplitude for current c. The phase difference between the current and the emf of the generator

Answer 1

(a) 14.88 ohm

(b) 1.88 A

(c) -74.4°

Step-by-step explanation:

Vo = 28 V

f = 12 kHz = 12000 Hz

R = 4 ohm

L = 30 micro henry = 30 x 10^-6 H

C = 800 nF = 800 x 10^-9 F

(a)

The inductive reactance,

XL = 2 π f L = 2 x 3.14 x 12000 x 30 x 10^-6 = 2.26 ohm

The capacitive reactance

`X_(c)=(1)/(2\pi fC)=(1)/(2 * 3.14 * 12000 * 800 * 10^(-9))`

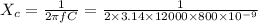
Xc = 16.59 ohm

Let the impedance is Z.

`Z=\sqrt{4^(2)+\left ( 2.26-16.59 \right )^(2)}`

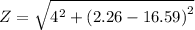
Z = 14.88 ohm

(b)

The formula for the amplitude of current

`I_(o)=(V_(o))/(Z)=(28)/(14.88)`

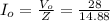
Io = 1.88 A

(c)

Let the phase difference is Ф

`tan\phi =(X_(L)-X_(C))/(R)=(2.26-16.59)/(4)=-3.5825`

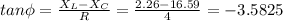
Ф = -74.4°