Question

The function f(x) = (x − 4)(x − 2) is shown. On a coordinate plane, a parabola opens up. It goes through (2, 0), has a vertex at (3, negative 1), and goes through (4, 0). What is the range of the function? All real numbers less than or equal to 3 all real numbers less than or equal to −1 all real numbers greater than or equal to 3 all real numbers greater than or equal to −1

Answer 1

Answer: all real numbers greater than it equal to negative one.

Step-by-step explanation: if you graph this equation you see that the vertex is at (3,-1). We know that Range is all possible Y values.so, By looking at their graph we can see that the lowest point it touches is at -1. The rest of the graph goes off into positive and negative infinity.

Range= Y is greater than it equal to -1.

Answer 2

All real numbers greater than or equal to −1

Explanation:

Here, the given parabola,

`f(x) = (x-4)(x-2)`

`f(x) = x^2-4x-2x + 8`

`f(x) = x^2 - 6x+8`

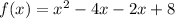
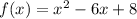
∵ Leading term = positive

So, the parabola is upward.

We know that an upward parabola is minimum at its vertex

Or it gives minimum output value at its vertex.

for instance, If (h, k) is the vertex of an upward parabola,

then its range = { x : x ≥ k, x ∈ R }

Note : Range = set of all possible output values

We have given,

Vertex = (3, -1)

Hence, Range = all real numbers greater than or equal to −1

LAST option is correct.