Question

a sewage treatment plant has two inlet pipes to its settling pond. one piece can fill the pond 3 times as fast as the other pipe, and together they can fill the pond in 12 hours. how long will it take the faster pipe to fill the pond alone

Answer 1

The faster pipe will take 16 hours to fill the pond alone

Explanation:

* Lets explain how to solve the problem

- A sewage treatment plant has two inlet pipes to its settling pond

- One pipe can fill the pond 3 times as fast as the other pipe

∴ The rate of the faster pipe is 3 times the rate of the second pipe

- The rate and the time are inverse proportion because;

time = job/rate and the job here is constant (fill pool), then

time × rate = constant

∵ The rate of the faster pipe is 3 times the rate of the second pipe

∴ The time of the second pipe is 3 times the time of the faster pipe

- Assume that the time of the faster pipe is t

∵ The time of the faster pipe is t

∴ The time of the second pipe is 3t

- Together they can fill the pond in 12 hours

∴
`(1)/(3t)+(1)/(t)=(1)/(12)`

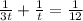
- The L.C.M of 3t and t is 3t

∴
`(1)/(3t)+(3)/(3t)=(1)/(12)`

∴
`(1+3)/(3t)=(1)/(12)`

∴
`(4)/(3t)=(1)/(12)`

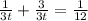
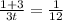
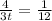
- By using cross multiplication

∴ 48 = 3t

- Divide both sides by 3

∴ t = 16

∵ t represents the time of the faster pipe

∴ The time of the first pipe is 16 hours

* The faster pipe will take 16 hours to fill the pond alone