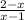Answer:
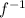 (x) =
(x) =
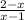
Explanation:
Let y = f(x) and rearrange making x the subject
y =
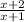 ( multiply both sides by (x + 1)
( multiply both sides by (x + 1)
y(x + 1) = x + 2 ← distribute left side
yx + y = x + 2 ( subtract x from both sides )
yx - x + y = 2 ( subtract y from both sides )
yx - x = 2 - y ← factor out x on the left side
x(y - 1) = 2 - y ← divide both sides by (y - 1 )
x =
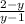
Change y back into terms of x, thus
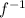 (x) =
(x) =