Question

Which ordered pair is part of the solution set of the inequality 12 + y ≤ –3x? Question 11 options: a) (3, –16) b) (4, –1) c) (–16, 3) d) (1, 4)

Answer 1

C (-16, 3)

Explanation:

`12 + 3 \leqslant - 3 * - 16 \\ 15 \leqslant 48`

replace x and y

Answer 2

c) (-16,3)

Explanation:

Given: inequality
`12+\text{y}\leq -3\text{x}`

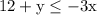
To Find: Which ordered pair is part of the solution set of the inequality

Solution:

Simplifying inequality,

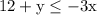
`12+\text{y}\leq -3\text{x}`

now,

putting ordered pairs from options

a)
`(3,-16)`

`-3*3-(-16)`
`16-9=7`

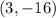
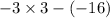
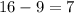
as
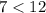`7<12`, it does not satisfy inequality

b)
`(4,-1)`

`-3*4-(-1)`
`1-12=-11`

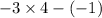
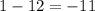
as
`-11<12`, it does not satisfy inequality

c)
`(-16,3)`

`-3*(-16)-(3)`
`48-3=45`

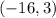
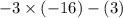
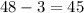
as
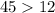`45>12`, it satisfy inequality

d)
`(1,4)`

`-3*1-(4)`
`-3-4=-7`

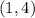
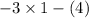
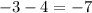
as
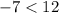`-7<12`, it does not satisfy inequality

So, from above only option c is part of the solution set of inequality.