Question

Find all solutions of each equation on the interval 0 ≤ x < 2π.

tan^2 x sec^2 x + 2sec^2 x - tan^2 x = 2

Answer 1

Explanation:

Answer 2

`x = 0` or
`x = \pi`.

Explanation:

How are tangents and secants related to sines and cosines?

`\displaystyle tan(x) = (sin(x))/(cos(x))`.

`\displaystyle \sec{x} = (1)/(cos(x))`.

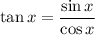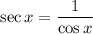Sticking to either cosine or sine might help simplify the calculation. By the Pythagorean Theorem,
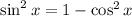`\sin^(2){x} = 1 - \cos^(2){x}`. Therefore, for the square of tangents,

`\displaystyle \tan^(2){x} = \frac{\sin^(2){x}}{\cos^(2){x}} = \frac{1 - \cos^(2){x}}{\cos^(2){x}}`.

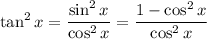This equation will thus become:

`\displaystyle \frac{1 - \cos^(2){x}}{\cos^(2){x}} \cdot \frac{1}{\cos^(2){x}} + \frac{2}{\cos^(2){x}} - \frac{1 - \cos^(2){x}}{\cos^(2){x}} = 2`.

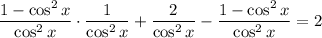To simplify the calculations, replace all
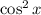`\cos^(2){x}` with another variable. For example, let
`u = \cos^(2){x}`. Keep in mind that
`0 \le \cos^(2){x} \le 1 \implies 0 \le u \le 1`.

`\displaystyle (1 - u)/(u^(2)) + (2)/(u) - (1 - u)/(u) = 2`.

`\displaystyle ((1 - u) + u - u \cdot (1- u))/(u^(2)) = 2`.

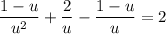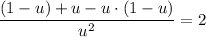Solve this equation for
`u`:

`\displaystyle (u^(2) + 1)/(u^(2)) = 2`.

`u^(2) + 1 = 2 u^(2)`.

`u^(2) = 1`.

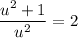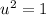Given that
`0 \le u \le 1`,
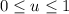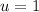`u = 1` is the only possible solution.

`\cos^(2){x} = 1`,

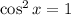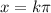`x = k \pi`, where
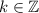`k\in \mathbb{Z}` (i.e.,
`k` is an integer.)

Given that
`0 \le x < 2\pi`,

`0 \le k <2`.

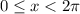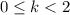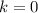`k = 0` or
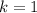`k = 1`. Accordingly,

`x = 0` or
`x = \pi`.