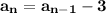Question

2. Find the common difference and the recursive formula. a. 22, 19, 16, 13, …

Answer 1

The common difference d is d = -3

The recursive formula is:
`\mathbf{a_n=a_(n-1)-3}`

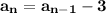
Explanation:

We need to find the common difference and the recursive formula.

a. 22, 19, 16, 13, …

First we will find common difference

The formula of arithmetic sequence is:
`a_n=a_1+(n-1)d`

where a_n is nth term, a_1 is 1st term and d is the difference

Looking at the sequence we get: a_1=22, a_2=19

Using these values we can find d, the common difference

`a_n=a_1+(n-1)d\\put\:n=2, a_2=19, a_1=22\\19=22+(2-1)d\\19=22+d\\d=19-22\\d=-3`

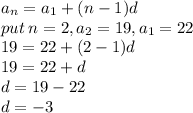
So, the common difference d is d = -3

Now, we will find the recursive formula:

The recursive formula is of type:
`a_n=a_(n-1)+d`

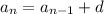
We have found common difference d = -3

So, the recursive formula will be:

`a_n=a_(n-1)+d\\a_n=a_(n-1)+(-3)\\a_n=a_(n-1)-3`

The recursive formula is:
`\mathbf{a_n=a_(n-1)-3}`