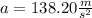Answer:
The acceleration from it's legs is
Step-by-step explanation:
Let's order the information:
Initial height:
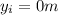
Final height:
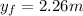
The bush accelerates from
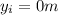 to
to
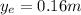 .
.
We can use the following Kinematic Equation to know the velocity at
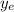 :
:
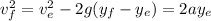
where g is gravity's acceleration (9.8m/s). Since
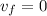 ,
,
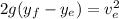
⇒

Working with the same equation but in the first height interval:
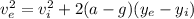
Since
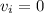 and
and
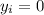 ,
,
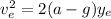
⇒
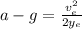
⇒
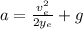 ⇒
⇒