Answer:
The value of a+b is 4.
Explanation:
The given function is
![\[f(x) = \left\{ \begin{array}{cl} 9 - 2x & \text{if } x \le 3, \\ ax + b & \text{if } x > 3. \end{array} \right.\]](https://img.qammunity.org/2020/formulas/mathematics/high-school/cdrv8gsrkk3lxh247ic3ng9j3fhtg2xdjz.png)
It is given that for some constants a and b the function f has the property that f(f(x))=x for all x.
For x≤3,
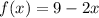
For x>3,
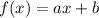
At x=0,

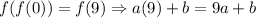
Using property f(f(x))=x,
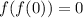
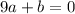 .... (1)
.... (1)
At x=1,

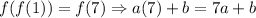
Using property f(f(x))=x,
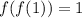
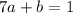 .... (2)
.... (2)
Subtract equation (2) from equation (1).
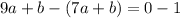
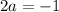
Divide both sides by 2.
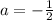
Substitute this value in equation (1).
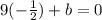
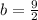
The value of a is
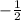 and value of b is
and value of b is
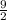 . The value of a+b is
. The value of a+b is
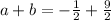
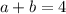
Therefore the value of a+b is 4.