7. When companies employ control charts to monitor the quality of their products, a series of small samples is typically used to determine if the process is "in control&quo…

Question

7. When companies employ control charts to monitor the quality of their products, a series of small samples is typically used to determine if the process is "in control" during the period of time in which each sample is selected. Suppose a concrete-block manufacturer samples nine blocks per hour and tests the breaking strength of each. During one-hour’s test, the mean and standard deviation are 985.6 pounds per square inch (psi) and 22.9 psi, respectively. a. Construct a 99% confidence interval for the mean breaking strength of blocks produced

Answer 1

A 99% confidence interval for the mean breaking strength of blocks produced is
`[959.987, 1011.213]`

Explanation:

A (1 -
`\alpha`)x100% confidence interval for the average break in these conditions It is an interval for the population mean with unknown variance and is given by:

`[\bar x -T_{(n-1,(\alpha)/(2))} (S)/(√(n)), \bar x +T_{(n-1,(\alpha)/(2))} (S)/(√(n))]`

`\bar X = 985.6psi`

`n = 9`

`\alpha = 0.01`

`T_{(n-1,(\alpha)/(2))}=3.355`

`S = 22.9`

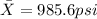
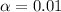
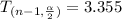
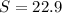
With this information the interval is determined by:

`[985.6 - 3.355(22.9)/(√(9)), [985.6 - 3.355(22.9)/(√(9))] = [959.987, 1011.213]`