Answer:
She needs 300 mililiters of Solution B so that the resulting mixture is a 12% alcohol
Explanation:
In this problem you have to take into account that when you are talking about solutions you can't just add the porcentaje because each percentaje represent how many mililiters of the total of the solution are, in this case of alcohol.
So for solving this problem we are first going to establish the variables, because it si solved using a system of equations. In that way we are going to say that:
VT: represents the total volume of the resulting mixture of solution A and solution B at 12% of alcohol
VA: represent the mililiters of solution A, in the problem they say that this value it equals to 400 ml
VB: Represent the mililiters of solution B, that is what we need to find.
From now on, we are just going to use this variables but always keep in mind what does they represent.
VaT: Represent the total volume of alcohol in the resulting mixture solution at 12%
VaA: Represent the volume of alcohol in solution A
VaB: Represent the volume of alcohol in solution B
What comes next? we need to describe the equations from the information we have so that we create a system that can be solve after.
What can we first say about the total volume (VT)? That it is the result of the adition of solution A and B so we can state the following equation:
VT = VA + VB
As we know that VA equals to 400ml we can replace to get:
1) VT = 400ml + VB
But what happens with the other information we have? We now need to take into account the concentration of each solution, so as we can´t add the percentages of alcohol but we can add the volumes of alcohol in each solution we can say that:
2) VaT = VaA + VaB
Now we are going to start to reduce the number of variables changing does that we don't know for those that we do to solve the problem, starting first with the volumes of alcohol.
A porcentaje represents a part of the total volume so to know how much alcohol does each of the solutions has we must do rules of three so that we can leave all the variables in terms of VT, VA and VB:
- VT → 100%
VaT → 12%
VaT =
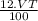 = 0,12.VT
= 0,12.VT
- VA → 100% In this case we know that VA = 400
VaA → 6%
VaA =

VaA =

VaA=24ml
VaB → 100%
VaB → 20%
VaB =
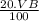 = 0,20.VB
= 0,20.VB
Now we are going to replace this information in the equation number two to get the following expresion:
3) 0,12.VT = 24ml + 0.20VB
At this point we have a system of two equations (remember equation 1) with two variables VT and VB so we are going to do some algebra to clear the variables.
- Replace VT of equation 1 in equation 3
Remeber that VT = 400ml + VB so now we are going to put this information in equation 3) 0,12.VT = 24ml + 0.20VB to get:
4) 0,12 (400ml + VB) = 24ml + 0.20VB
- Use the distributive operation to solve the parentesis
0,12x400ml + 0.12.VB = 24ml + 0.20VB
5) 48ml + 0.12VB = 24ml + 0.20VB
- Organize the information in one side the ones with variables and in the other side just numbers:
0.12VB - 0.20VB = 24ml - 48ml
-0.08 VB = -24ml (do the operations)
As it is a minus in both sides we can divide it and cancel the sign to have:
0,08VB = 24 ml (to clear VB, we must divide in both sides by 0,08)
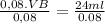 after doing the division we get:
after doing the division we get:
VB = 300ml
with this you already get the answer of how many mililiters of solution B does she use to get a resulting mixture of 12%.
To verficate we must do the following process:
VT = 300ml + 400ml = 700ml
The total volume of the solution is 700 ml of which 12% equals to:
VaT = 0,12. VT = 0,12(700ml) = 84 ml
VaA = 24ml (Volume of alcohol in solution A, we already calculated)
VaB = 0,20 VB = 0,20(300ml) = 60ml (Volume of alcohol in solution B)
VaT = VaA + VaB (Prove the equation with the values we obtain)
84ml = 24ml + 60ml
84 ml = 84ml
As the equation is the same we have verificated our result.