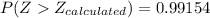Answer:
The level of significance observed is 0.99154
Explanation:
Assuming that in a sample of size 50 people stated that they do not like the snack (p = 17/50), you have:
Proportion in the null hypothesis

Sample size

Sample proportion
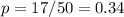
The expression for the calculated statistic is:
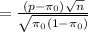
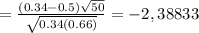
The level of significance observed is obtained from the value of the statistic calculated: