Question

A plane is flying horizontally with speed 167 m/s at a height 4040 m above the ground, when a package is dropped from the plane. The acceleration of gravity is 9.8 m/s 2 . Neglecting air resistance, when the package hits the ground, the plane will be:

Answer 1

The plane will be 4795.23 meters from where he threw the package.

Step-by-step explanation:

Data:

v = 167 m/s

h = 4040 m

g = 9.8m/s²

package:

after it is dropped there is no horizontal force, so...

`X - Xo = Vt`

t =
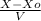`(X - Xo)/(V)` I

in the vertical we have only
`P = mg`

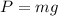
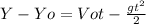`Y - Yo = Vot -(gt^(2) )/(2)` but Vo = 0 because the package is dropped

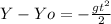`Y - Yo =-(gt^(2) )/(2)` II

replacing I in II

`Y - Yo =-(g(X - Xo)^(2) )/(2V^(2))`

`0 - 4040 =-(9.8(X - Xo)^(2) )/(2*167^(2))`

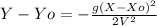
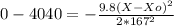
X - Xo = 4795.23

The distance from where the plane drops the package and where it hits the ground is the same as the plane flies horizontally, as there is no acceleration at x.