Answer: One 8-cm pipe (Its is greater than the total area of of two 4-cm pipes)
Explanation:
The area of a circle can be calculate with this formula:
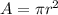
Where "r" is the radius of the circle.
We need to calculate the area of 8-cm pipe. In this case:
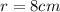
Then, substituting the radius into the formula, we get:
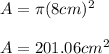
Now we must calculate the area of the two 4-cm pipes.
Since they are two pipes, the formula is:
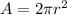
In this case:

Then, substituting into the formula, we get:

Therefore, since the area of one 8-cm pipe is greater than the total area of of two 4-cm pipes, we conclude that the pipe configuration that can deliver more water to residents is:
One 8-cm pipe