Question

For what values of b are the vectors \langle -46, b, 10 \rangle and \langle b, b^2, b \rangle orthogonal

Answer 1

b = 6 or b = -6 (non-zero vectors)

b = 0 (zero vector)

Explanation:

Two vectors
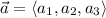`\vec{a}=\langle a_1,a_2,a_3\rangle` and
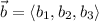`\vec{b}=\langle b_1,b_2,b_3\rangle` are orthogonal if their dot product is equal to 0, or in other words

`a_1\cdot b_1+a_2\cdot b_2+a_3\cdot b_3=0`

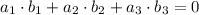
In your case,

`\vec{a}=\langle -46, b, 10\rangle\\ \\\vec{b}=\langle b,b^2,b\rangle`

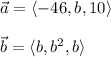
Hence, if vectors a and b are orthogonal, then

`-46\cdot b+b\cdot b^2+10\cdot b=0\\ \\-46b+b^3+10b=0\\ \\b^3-36b=0\\ \\b(b^2-36)=0\\ \\b(b-6)(b+6)=0\\ \\b=0\text{ or }b=6\text{ or }b=-6`

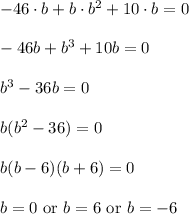
Note, then if b = 0, then
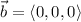`\vec{b}=\langle 0,0,0\rangle` and zero-vector is orthogonal to any other vectors.

Thus, b = 6 or b = -6.