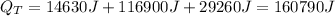Question

How much heat is necessary to change 350 g of ice at -20 degrees Celsius to water at 20 Celsius?

Answer 1

160790 J

Step-by-step explanation:

We can find the heat necessary for the ice to go from -20 degrees Celsius to 0 degrees Celsius:

`Q=mc\Delta t`

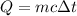
Where
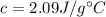`c=2.09 J/g^(\circ)C` is the specific heat of ice, that is the amount of heat that must be supplied per unit mass to raise its temperature in a unit.

`Q=(350g)(2.09 J/g^(\circ)C)(0^(\circ)C-(-20^(\circ)C))=14630 J`

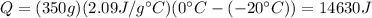
We must calculate the latent heat of fusion required for this ice mass to change to water:

`Q=mH`

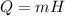
Where H=334 J/g is the specific latent heat of fusion of water, that is the amount of energy needed per unit mass of a substance at its melting point to change from the solid to the liquid state.

`Q=(350g)(334 J/g)=116900 J`

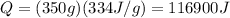
Then we calculate the heat necessary for the water to go from 0 degrees Celsius to 20 degrees Celsius:

`Q=mc\Delta t`

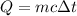
Where
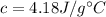`c=4.18 J/g^(\circ)C` is the specific heat of water, that is the amount of heat that must be supplied per unit mass to raise its temperature in a unit.

`Q=(350g)(4.18 J/g^(\circ)C)(20^(\circ)C-0^(\circ)C)=29260 J`

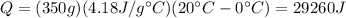
Finally the 3 results are added:

`Q_(T)=14630 J + 116900 J + 29260 J=160790 J`