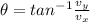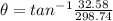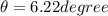Answer:
Speed of plane is 300.5 m/s at angle of 6.22 degree South of West
Step-by-step explanation:
Air speed of the plane is given as
v = 264 m/s in direction 5 degree South of West
So we have
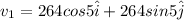
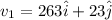
Also we have speed of air is given as
v = 37 m/s at 15 degree South of West
so it is
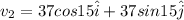
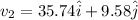
So the net speed of plane with respect to ground is given as
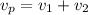
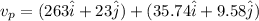
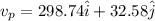
so it is
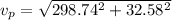
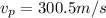
direction is given as