Answer:
The properties of reflection are used when we want to reflect a figure across a specific line, it can be across y-axis, x-axis, y = x or y = -x.
In either case, the result is a reflection, that is, those lines will work as a mirror, having the same shape and size but reflected across the line.
It's important to say that a reflection is a rigid transformation, which means the shape or size of the figure won't chance.
If we want to reflect across the y-axis, the transformation is:

Across the x-axis:
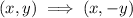
Across the line y = x:
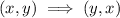
Across the line y = -x:
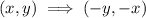 .
.