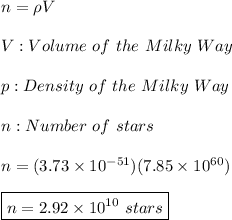Question

The distance from the Sun to the nearest star is about 4 ✕ 1016 m. The Milky Way galaxy is roughly a disk of diameter ~ 1021 m and thickness ~ 1019 m. Find the order of magnitude of the number of stars in the Milky Way. Assume the distance between the Sun and our nearest neighbor is typical.

Answer 1

`\boxed{n=2.92* 10^(10) \ stars}`

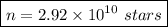
Step-by-step explanation:

Order-of-magnitude estimates are useful when we want to get a very crude estimate of a quantity. Sometimes, to get the exact calculation of a problem is very difficult, or impossible, so we use order of magnitud in order to get a rough approximation. In this exercise, we need to find the order of magnitude of the number of stars in the Milky Way. We know:

The distance from the Sun to the nearest star is:

`4 * 10^(16)m`

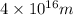
The Milky Way galaxy is roughly a disk of diameter:

`10^(21)`

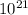
The Milky Way galaxy is roughly a disk of thickness:

`10^(19)`

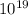
So we can approximate volume of the Milky Way:

`V=\pi r^2 h \\ \\ r=(10^(21))/(2)m=5 * 10^(20)m \\ \\ h=10^(19)m \\ \\ \\ V=\pi(5 * 10^(20))^2(10^(19)) \\ \\ V=7.85* 10^(60)m^3`

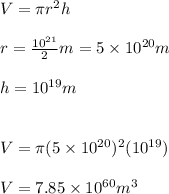
Now, let's estimate a rough density for the Milky Way. It is well known that in a sphere with a radius of
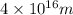`4* 10^(16)m` there is a star, which is the sun. So the density of the Milky way is:

`\rho =(n)/(V) \\ \\ \rho:Density \ of \ Milky \ way \\ \\ n: Number \ of \ stars \\ \\ V:Volume`

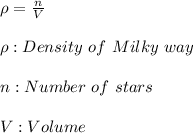
For one star
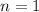`n=1` so we know the data at the neighborhood around the Sun, so the volume is a sphere:

`V=V_(sphere)=(4)/(3)\pi r^3 \\ \\ V_(sphere)=(4)/(3)\pi (4* 10^(16))^3 \\ \\ V_(sphere)=2.68* 10^(50)m^3 \\ \\ So: \\ \\ \rho=(1)/(2.68* 10^(50))=3.73* 10^(-51)stars/m^3`

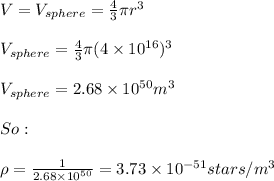
Finally, the numbers of stars can be found as:

`n=\rho V \\ \\ V:Volume \ of \ the \ Milky \ Way \\ \\ p:Density \ of \ the \ Milky \ Way \\ \\ n:Number \ of \ stars \\ \\ n=(3.73* 10^(-51))(7.85* 10^(60)) \\ \\ \boxed{n=2.92* 10^(10) \ stars}`