Step-by-step explanation:
Given that,
Wavelength of the laser light,
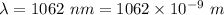
The laser pulse lasts for,
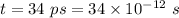
(a) Let d is the distance covered by laser in the given by,
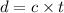
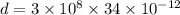
d = 0.0102 meters
Let n is the number of wavelengths found within the laser pulse. So,
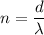
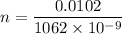
n = 9604.51
(b) Let t is the time need to be fit only in one wavelength. So,
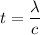
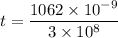
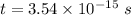
Hence, this is the required solution.