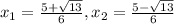Answer:
The solutions of the quadratic equation are
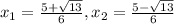
Explanation:
This is a second order polynomial, and we can find it's roots by the Bhaskara formula.
Explanation of the bhaskara formula:
Given a second order polynomial expressed by the following equation:
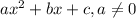 .
.
This polynomial has roots
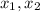 such that
such that
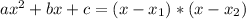 , given by the following formulas:
, given by the following formulas:
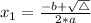
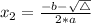
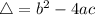
For this problem, we have to find
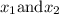 .
.
The polynomial is
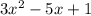 , so a = 3, b = -5, c = 1.
, so a = 3, b = -5, c = 1.
Solution
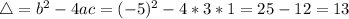
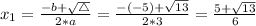
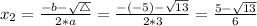
The solutions of the quadratic equation are