Question

The captain orders his starship to accelerate from rest at a rate of "1 g" (1 g = 9.8 m/s2). How many days does it take the starship to reach 5% the speed of light?

(Light travels at 3.0 × 10^8 m/s.)

Answer 1

17.7 days

Step-by-step explanation:

Since the ship accelerates from the rest, its initial velocity would be equal to 0.

So,

`v_(i)=0`

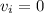
Acceleration of the star-ship = a = 1 g = 9.8 m/s²

We need to find how many days will it take the ship to reach 5% of the speed of light. Speed of light is
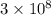`3 * 10^(8)` m/s.

5% of the speed of light =
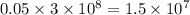`0.05 * 3 * 10^(8)=1.5* 10^(7)` m/s

This means, the final velocity of the star-ship will be:

`v_(f)=1.5* 10^(7)`

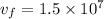
We have the initial velocity, final velocity and the acceleration. We need to find the time(t). First equation of motion relates these quantities as:

`v_(f)=v_(i)+at`

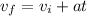
Using the values in this equation, we get:

`1.5 * 10^(7)=0+9.8(t)\\\\ t=(1.5*10^(7))/(9.8)\\\\ t=1,530,612.245`

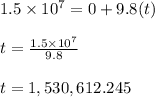
Thus, the star-ship will take 1,530,612.245 seconds to reach to 5% the speed of light. Now we need to convert this time to days.

Since, there are 60 seconds in a minute:

1,530,612.245 seconds =
`(1,530,612.245)/(60)=25510.20` minutes

Since, there are 60 minutes in an hour:

25,510.20 minutes =
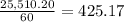`(25,510.20)/(60)=425.17` hours

Since, there are 24 hours in a day:

425.17 hours =
`(425.17)/(24)=17.7` days

Thus, it will take approximately 17.7 days (approximately 17 days and 17 hours) to reach to 5% the speed of light