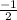Answer:
Explanation:
General form of equation of line =

Where m is the slope of line
We are given a line
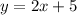
On comparing with general form
m = 2
Let n be the slope of line perpendicular to the line
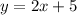
The product of the slopes of perpendicular lines is -1
So,
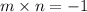
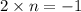
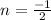
So, Option B is correct
Hence the slope of a line perpendicular to the line whose equation is y=2x + 5 is