Question

Can someone explain to me how to do questions 6-8 because I understand how to do 3-5 now. Can you explain to me how you do this please ? I have a test tomorrow

Answer 1

see explanation

Explanation:

Using the midpoint formula to equate the x and y coordinates of the endpoints to the x and y coordinates of the midpoint, that is

(6)

let ( x, y ) be the coordinates of the required endpoint, then

x →
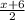`(x+6)/(2)` = 2 ( multiply both sides by 2 )

x + 6 = 4 ( subtract 6 from both sides )

x = - 2 and

y →
`(y+2)/(2)` = 0 , thus

y + 2 = 0 ( subtract 2 from both sides )

y = - 2

Coordinates of the other endpoint = (- 2, - 2)

(7)

x →
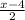`(x-4)/(2)` = - 1 ( multiply both sides by 2 )

x - 4 = - 2 ( add 4 to both sides )

x = 2 and

y→
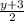`(y+3)/(2)` = - 1 ( multiply both sides by 2 )

y + 3 = - 2 ( subtract 3 from both sides )

y = - 5

Coordinates of the other endpoint = (2, - 5)

(8)

x →
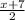`(x+7)/(2)` = 2 ( multiply both sides by 2 )

x + 7 = 4 ( subtract 7 from both sides )

x = - 3 and

y →
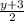`(y+3)/(2)` = 1 ( multiply both sides by 2 )

y + 3 = 2 ( subtract 3 from both sides )

y = - 1

Coordinates of the other endpoint = (- 3, - 1)

Answer 2

Answer: 6. 4,2

7. 3,2

8. 5,2

please forgive me if i am incorrect.