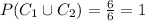Question

A positive integer from one to six is to be chosen by casting a die. Thus the elements c of the sample space C are 1, 2, 3, 4, 5, 6. Suppose C1 = {1, 2, 3, 4} and C2 = {3, 4, 5, 6}. If the probability set function P assigns a probability of 1 6 to each of the elements of C, compute P(C1), P(C2), P(C1 ∩ C2), and P(C1 ∪ C2).

Answer 1

Answer with Step-by-step explanation:

We are given that six integers 1,2,3,4,5 and 6.

We are given that sample space

C={1,2,3,4,5,6}

Probability of each element=
`(1)/(6)`

We have to find that
`P(C_1),P(C_2),P(C_1\cap C_2) \;and\; P(C_1\cup C_2)`

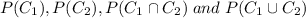
Total number of elements=6

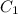`C_1`={1,2,3,4}

Number of elements in
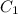`C_1`=4

`P(E)=(number\;of\;favorable \;cases)/(Total;number \;of\;cases)`

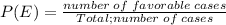
Using the formula

`P(C_1)=(4)/(6)=(2)/(3)`

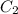`C_2`={3,4,5,6}

Number of elements in
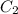`C_2`=4

`P(C_2)=(4)/(6)=(2)/(3)`

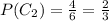
`C_1\cap C_2`={3,4}

Number of elements in
`(C_1\cap C_2)=2`

`P(C_1\cap C_2)=(2)/(6)=(1)/(3)`

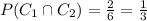
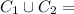`C_1\cup C_2=`{1,2,3,4,5,6}

`P(C_1\cup C_2)=(6)/(6)=1`