Question

You are traveling on an airplane. The velocity of the plane with respect to the air is 140 m/s due east. The velocity of the air with respect to the ground is 31 m/s at an angle of 30° west of due north. 1) What is the speed of the plane with respect to the ground?

Answer 1

127.36 m/s

Step-by-step explanation:

velocity of plane with respect to air = 140 m/s due east

velocity of air with respect to ground = 31 m/s 30° west of north

Write the velocities in the vector forms

`\overrightarrow{V_(p/a)}=140\widehat{i}`

`\overrightarrow{V_(a/g)}=31  \left ( -Sin30 \widehat{i}+Cos30\widehat{j} \right )`

`\overrightarrow{V_(a/g)}= -15.5 \widehat{i}+26.85\widehat{j}`

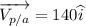
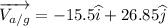
Let velocity of plane with respect to ground is given by vp/g

According to the formula of relative velocities

`\overrightarrow{V_(p/a)}=\overrightarrow{V_(p/g)}-\overrightarrow{V_(a/g)}`

`\overrightarrow{V_(p/g)}=\overrightarrow{V_(p/a)}+\overrightarrow{V_(a/g)}`

`\overrightarrow{V_(p/g)}= \left ( 140-15.5 \right )\widehat{i}+26.85\widehat{j}`

`\overrightarrow{V_(p/g)}= \left ( 124.5 \right )\widehat{i}+26.85\widehat{j}`

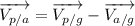
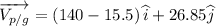
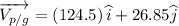
The magnitude of the velocity of plane with respect to the ground is given by

`V_(p/g) = \sqrt{124.5^(2)+26.85^(2)}=127.36 m/s`

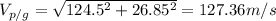
Thus, the velocity of plane with respect to the ground is given by 127.36 m/s.